一、概念
1、是一课二叉查找树。（每个节点都是唯一的）
2、每个节点左右子节点高度差不超过1。

二叉查找树为了查找方便我们会将所有左右子节点统一设置规则左小右大，或者反之。
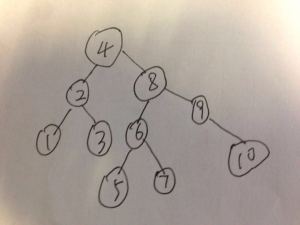
假定左小右大，将1-10的数字插入二叉平衡树 则结果为：

二、树的遍历

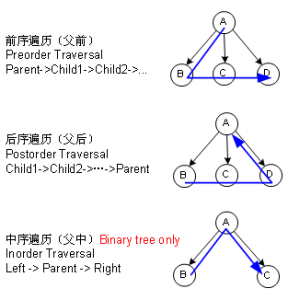
常用树的遍历顺序有3种，分别为：先序（前序）、中序、后序

上述二叉树采用三种遍历方式分别得到结果
先序：4 2 1 3 8 6 5 7 9 10
中序：1 2 3 4 5 6 7 8 9 10 (可以看出平衡二叉树 中序遍历就是一个排好顺的结果)
后序: 1 3 2 5 7 6 10 9 8 4

三、结构

每个树节点都应该拥有自身值和左右两个节点（末端节点会没有子节点或只有一个子节点）。为了方便我们还讲在节点上储存记录当前节点的高。 结构如下：

struct AVLTreeNode
{
    int value; //节点存储的值
    struct AVLTreeNode* leftNode;  //左子节点
    struct AVLTreeNode* rightNode; //右子节点
    int height; //节点高
};

四、操作
AVL在插入和删除节点可能会造成树的不平衡（左右子节点高度差超过1），调整方法为旋转，根据不同平衡结构可以分为: LL型(左左)、RR型(右右)、LR、RL。对应进行旋转。

如下图为LL型，在B节点子树上插入节点A节点失衡。调整过程为：以B节点为轴心，A节点顺时针旋转至B节点的右子树，A的右子树用B的又子树代替。通过旋转使B节点为根的平衡子树。RR和LL成对应关系，操作方向相反即可。

下图为LR结构，在B节点的右子树上出插入新的节点A节点失衡，调整过程为：首先以C为轴心，B绕C逆时针旋转，生成的子树这样就成为了LL型，然后用上述方法调整即可，通过先左后右旋转，是使C成为根节点的平衡子树，RL和RL成对应关系，操作方向相反即可

LL：单右旋

RR: 单左旋

LR ：先左旋后右旋

RL：先右旋后左旋。

代码实现

//
//  AVLTree.h
//  AVLTree
//

#ifndef AVLTree_h
#define AVLTree_h

#include 

enum EACH_ORDER
{
    EACH_ORDER_PRE,     //先序
    EACH_ORDER_POST,    //后序
    EACH_ORDER_MID,     //中序
};

typedef struct AVLTreeNode* AVLTree;

struct AVLTreeNode
{
    int value;
    AVLTree leftNode;
    AVLTree rightNode;
    int height;
};

//释放
AVLTree avl_free(AVLTree tree);

//插入
AVLTree avl_insertValue(int value, AVLTree tree);

//查找
AVLTree avl_find(int value, AVLTree tree);
AVLTree avl_findMin(AVLTree tree);
AVLTree avl_findMax(AVLTree tree);

//旋转
AVLTree avl_rotateRight(AVLTree tree);
AVLTree avl_rotateLeft(AVLTree tree);
AVLTree avl_doubleRotateRight(AVLTree tree);
AVLTree avl_doubleRotateLeft(AVLTree tree);

void  avl_printTree(enum EACH_ORDER order, AVLTree tree);


#endif /* AVLTree_h */

//
//  AVLTree.c
//  AVLTree
//
//

#include "AVLTree.h"
#include <stdlib.h> 

#define max(x,y)  ( x>y?x:y )


int avl_height(AVLTree tree)
{
    return (tree == NULL) ? -1 : tree->height;
}


AVLTree avl_free(AVLTree tree)
{
    if (tree != NULL)
    {
        avl_free(tree->leftNode);
        avl_free(tree->rightNode);
        free(tree);
    }
    return NULL;
}



void    avl_printTree(enum EACH_ORDER order, AVLTree tree)
{
    if(tree == NULL)
    {
        return;
    }
    
    if( order == EACH_ORDER_PRE ) printf("%d ", tree->value);
    
    avl_printTree(order, tree->leftNode);
    
    if( order == EACH_ORDER_MID ) printf("%d ", tree->value);
    
    avl_printTree(order, tree->rightNode);
    
    if( order == EACH_ORDER_POST ) printf("%d ", tree->value);
}




AVLTree avl_find(int value, AVLTree tree)
{
    if(tree == NULL)
    {
        return NULL;
    }
    if(value < tree->value)
    {
        return avl_find(value, tree->leftNode);
    }
    else if(value > tree->value)
    {
        return avl_find(value, tree->rightNode);
    }
    return tree;
}


AVLTree avl_findMin(AVLTree tree)
{
    if(tree==NULL)
    {
        return NULL;
    }
    
    if(tree->leftNode==NULL)
    {
        return tree;
    }
    return avl_findMin(tree->leftNode);
}


AVLTree avl_findMax(AVLTree tree)
{
    if(tree==NULL)
    {
        return NULL;
    }
    
    if(tree->rightNode==NULL)
    {
        return tree;
    }
    return avl_findMax(tree->rightNode);
}



AVLTree avl_insertValue(int value, AVLTree tree)
{
    if(tree==NULL)
    {
        tree =  (struct AVLTreeNode*)malloc(sizeof(struct AVLTreeNode));
        if( tree == NULL )
        {
            printf("out of space");
        }
        
        tree->value = value;
        tree->leftNode = NULL;
        tree->rightNode = NULL;
        tree->height = 0;
    }
    
    else if(value < tree->value)
    {
        tree->leftNode = avl_insertValue(value, tree->leftNode);
        
        if( avl_height(tree->leftNode) -  avl_height(tree->rightNode)  == 2)
        {
            if( value < tree->leftNode->value)
            {
                tree = avl_rotateLeft(tree);
            }
            else
            {
                tree = avl_doubleRotateLeft(tree);
            }
        }
    }
    
    else if(value > tree->value)
    {
        tree->rightNode = avl_insertValue(value, tree->rightNode);
        
        if( avl_height(tree->rightNode) - avl_height( tree->leftNode ) == 2)
        {
            if( value > tree->rightNode->value)
            {
                tree = avl_rotateRight(tree);
            }
            else
            {
                tree = avl_doubleRotateRight(tree);
            }
        }
    }
    else
    {
        printf("node is existed");
    }
    
    tree->height = max( avl_height(tree->leftNode),
                           avl_height(tree->rightNode)) + 1;

    return tree;
}














AVLTree avl_rotateLeft(AVLTree k2)
{
    if(k2==NULL)
    {
        return NULL;
    }
    
    if(k2->leftNode ==NULL)
    {
        return k2;
    }
    
    AVLTree k1 = k2->leftNode;
    k2->leftNode = k1->rightNode;
    k1->rightNode = k2;
    
    k2->height = max( avl_height(k2->leftNode), avl_height(k2->rightNode) ) + 1;
    k1->height = max( avl_height(k1->leftNode), k2->height )  + 1 ;
    
    return k1;
}

AVLTree avl_rotateRight(AVLTree k2)
{
    if(k2==NULL)
    {
        return NULL;
    }
    
    if(k2->rightNode ==NULL)
    {
        return k2;
    }
    
    AVLTree k1 = k2->rightNode;
    k2->rightNode = k1->leftNode;
    k1->leftNode = k2;
    
    k2->height = max( avl_height(k2->rightNode), avl_height(k2->leftNode) )  + 1;
    k1->height = max( avl_height(k1->rightNode), k2->height ) + 1;
    
    return k1;
}





AVLTree avl_doubleRotateRight(AVLTree tree)
{
    tree->rightNode = avl_rotateLeft(tree->rightNode);
    return avl_rotateRight(tree);
}


AVLTree avl_doubleRotateLeft(AVLTree tree)
{
    
    tree->leftNode = avl_rotateRight(tree->leftNode);
    return avl_rotateLeft(tree);
}